
A low cholesterol diet is definitely a must nowadays. After all, your cholesterol and health go hand in hand. Eating too much high cholesterol food can give way to diseases like hyperlipidemia, which increases your risk of heart problems as you grow older.
Thankfully, there are easy ways to avoid this unhealthy future. One of these includes eating healthy food that lowers cholesterol levels in your body. So in this article, we show you just how to lower cholesterol naturally with the help of our low cholesterol recipes!
Why Low Cholesterol Diet?![Why Low Cholesterol Diet]()
Why a low cholesterol diet? What does my diet have to do with my LDL cholesterol levels anyway? Some may not know it, but high cholesterol and heart disease are actually linked.
Cholesterol in itself isn’t bad. In fact, there are certain foods that naturally contain it, from egg yolk to cheese and even sardines. However, there are different kinds of cholesterol that are actually bad for your health. Some foods contain this bad cholesterol, and so eating this specific kind of high cholesterol diet can negatively affect one’s health.
But first, what is cholesterol anyway? And how does one’s diet affect its levels in your body?
What Is Cholesterol?

Cholesterol is a type of fatty, waxy substance that you can find in the cells of your body. It’s actually important in maintaining your overall health since it helps digest the food you eat. While your body makes this substance naturally, certain foods also contain cholesterol.
So if it’s natural, what’s the need for a low cholesterol diet? The problem actually lies in having too many of the bad kind.
Kinds of Cholesterol
There are three kinds of cholesterol: these are the HDL (high-density lipoprotein), LDL (low-density lipoprotein), and VLDL (very low-density lipoprotein)
HDL is “good cholesterol”, but LDL and VLDL are both considered as “bad cholesterol”. That’s because having high levels of LDL and VLDL can actually be harmful to your health.
Why Is High Cholesterol Bad For Your Health?

Having high VLDL and LDL cholesterol levels in your body can form “plaque”, which sticks to the walls of your arteries. This can build up and make them narrow or even blocked, preventing the blood from flowing to your heart. This may lead to you developing heart diseases, heart attacks, and even stroke.
While food like egg yolk and cheese contain cholesterol, it isn’t usually the bad kind. It’s the fried foods, fast foods, processed meats, and certain desserts that are actually high cholesterol foods.
How much cholesterol per day should you consume, then? Research shows that healthy people should only be consuming 300 milligrams of cholesterol per day. Those with already high cholesterol levels and diabetes should only have 200 milligrams daily. For reference, a single egg yolk already has 186 milligrams of cholesterol.
So if you’re wondering about how to reduce cholesterol levels in your body, then look no more. We’ll show you how to lower bad cholesterol levels with the help of our low cholesterol food list!
35 Low Cholesterol Recipes for a Heart-Healthy Diet
Those looking after their health should try their hand at the low cholesterol recipes we listed below. For this list, we picked healthy food recipes that feature ingredients that can help lower high cholesterol levels. So get ready to eat healthy with our 35 low cholesterol diet recipes!
Low Cholesterol Meatloaf
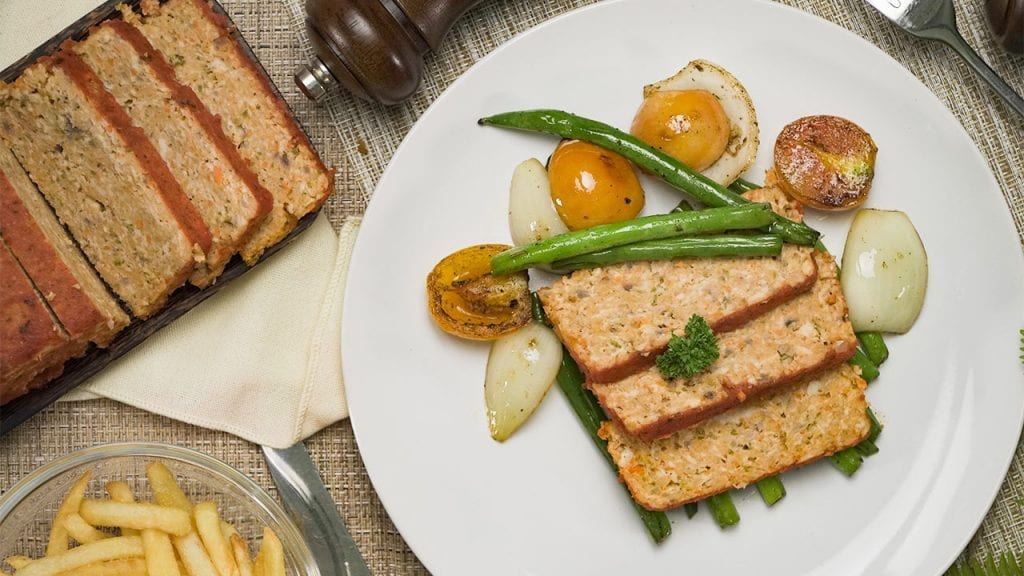
First on this list is our Low Cholesterol Meatloaf recipe. When people think “healthy”, they probably only picture themselves eating fruits, green veggies, and plant-based food like tofu all day. However, that’s not the case for this recipe. Thanks to this special recipe, even those with already high cholesterol can enjoy meat without worrying or feeling guilty.
Meatloaf is a classic dish that is a comfort food for many. It’s perfect for cozy dinners with family and friends. This meatloaf recipe is special because of its low cholesterol content. In this recipe, we avoid processed meats and use fresh, ground beef for the base. We also include low-cholesterol foods like oats and carrots. Whole grains, like oats, are healthy for the heart; research has shown that eating such foods lowers your risks of getting a heart disease. Meanwhile, carrots are pectin-rich vegetables that can help lower high cholesterol levels.
While it’s true that most meatloaf recipes use an oven for baking the dish, there are some recipes that let home chefs fry their meatloaf. Fortunately, this recipe bakes the meatloaf instead of frying it. This is important since fried foods are also one of the high sources of bad cholesterol.
Recipe for Inspiration: Low Cholesterol Meatloaf
Chilled Avocado Soup

Another healthy food with low cholesterol is the tasty avocado. This green fruit tastes amazing in salads and dessert, but nothing beats our chilled Avocado Soup. This delicious soup is refreshing not just because it’s eaten cold, but because it also uses fresh ingredients. It’s also quick and easy to make! All you have to do is puree the ingredients, chill the mixture for 2 hours, and voila! You have your tasty and healthy avocado soup.
Avocado is a great soup base because of its mild but delicious taste. However, its flavor isn’t the only thing going for this green fruit. Avocados are so rich in nutrients that they’re even considered as a superfood. This fruit is rich in vitamins, nutrients, and healthy fats that can help lessen your chances of getting cancer. In terms of cholesterol, avocados also have monounsaturated fats and fiber. These two kinds of nutrients are good at lowering bad cholesterol and great at increasing good cholesterol. Asides from avocado, you’ll also taste lemon, low-fat plain yogurt, radishes, and spices.
Nowadays, you can buy avocados at groceries even when they’re not in season. Coupled with how easy it is to make, and considering how delicious this dish tastes, there are many good reasons for you to try our avocado soup. It’s a dish that’s perfect for quick, working lunches.
Recipe for Inspiration: Chilled Avocado Soup
Broccoli Almond

Another delicious yet healthy green dish is our Broccoli Almond recipe. Although this recipe may seem simple, its taste is anything but. In this recipe, we make use of a healthy green vegetable like broccoli, and combine it with a low cholesterol food like almond nuts. While this dish is great for those looking for low cholesterol meals, it’s also a perfect way to serve lovely, warm green veggies for lunch or dinner. The broccoli is sauteed together with almond nuts, garlic, butter, and chicken broth to give it a rich, full flavor. While you can eat it alone as a main dish, it’s also great paired with savory dishes like the Chicken Asparagus Stroganoff.
Broccoli is a healthy green vegetable that’s a good source of fiber, protein, iron, calcium, and vitamins A, C, E, K and B. While it’s not really known for its low cholesterol levels, its soluble fiber can lower cholesterol levels in the same way that whole grain like oats do. Meanwhile, nuts, specifically almond and walnuts, are high in monounsaturated fats just like avocados. These fats can also lessen bad cholesterol levels and raise good cholesterol levels. Nuts also have minerals like calcium, magnesium, and potassium which can help boost overall heart health.
This Broccoli Almond dish is easy and affordable to make, with only a few ingredients and even fewer cooking instructions. It is great as both a light lunch, or a side dish. After making this dish, you’ll realize just how well the firm broccoli goes with crunchy and tasty almond nuts.
Recipe for Inspiration: Broccoli Almond
Bean Salad with Pine Nuts and Feta

Our Bean Salad with Pine Nuts and Feta is another nutty dish that’s safe to eat for those looking after their cholesterol levels. Asides from main dishes and soups, we also have a tasty salad recipe that uses certain foods to lower cholesterol. In this recipe, we feature beans, pine nuts, and feta cheese that are as nutritious as they are delicious. In addition, this recipe also uses onions, bell peppers, cucumber, parsley, olives, and honey to make the best-tasting, healthy salad for breakfast, lunch, or even dinner. It’s quick and easy to prepare, so busy bees with no time to spare can make this dish when they’re short on time. Just toss the ingredients in a bowl and you’re ready to eat.
Legumes, which are a group of plant foods that include beans, peas, and lentils, can lessen the amount of bad cholesterol in your body. The two types of beans used in this salad are kidney beans and pinto beans. Both have zero cholesterol, and are rich in fiber, protein, vitamins, and nutritious minerals. Eating kidney beans can even help regulate blood sugar levels, while pinto beans are great for your heart’s health. Pine nuts, like almonds and walnuts, are also able to lower bad cholesterol levels while raising the amount of good cholesterol. Meanwhile, feta cheese is high in phosphorus, iron, zinc, potassium, and vitamins A and B6.
If you’re craving for some refreshing salad, our Bean Salad with Pine Nuts and Feta Recipe is perfect. It’s nutritious, safe for those with high cholesterol, and absolutely scrumptious. This salad also goes well paired with healthy pasta dishes like our low-fat Tomato Pasta Salad.
Recipe for Inspiration: Bean Salad with Pine Nuts and Feta
Sugar-Free Apple Pie

Who says you can’t enjoy sweet desserts when you’re on a strict diet? With our Sugar-Free Apple Pie recipe, you won’t have to worry about your cholesterol or your blood sugar levels. This sweet and soft apple pie lets you eat yummy dessert without guilt, thanks to its lack of sugar and use of healthy ingredients.
Also, even though it doesn’t use sugar, this apple pie tastes just as amazing as other apple pie recipes that do use sugar. The only difference is that this one is healthier. Thanks to its cinnamon nutmeg spice and apple juice concentrate, this apple pie manages to keep its sweet and tart taste. And most importantly, this recipe is simple and easy to do. You won’t have to be an expert at baking to master this pie recipe. In just 5 easy steps, you have yourself a hot, piping apple pie that’s safe for diabetics and those with high cholesterol.
Although this dish is a dessert, its use of apples makes it safe for those looking after their cholesterol levels. Fruits–like apples, grapes, and citrus produce–as well as berries are rich in soluble fiber which can help lower cholesterol in your body. It does this by stopping your liver from producing its own natural cholesterol. When eaten, apples can actually lessen cholesterol by up to 10%! Also, fruits generally have important compounds that help stave off heart diseases.
This Sugar-Free Apple Pie Recipe is a great and healthy way to serve dessert that everyone can enjoy. Loved ones both young and old can experience the delectable taste of a good ‘ol apple pie right after enjoying a hearty meal.
Recipe for Inspiration: Sugar-Free Apple Pie
Citrus Glazed Salmon with Pecan-Citrus Rice

Good news! You can still enjoy rich, seafood like mackerel and salmon even when you’re on a low cholesterol diet. And in this recipe, we make dinner fancier and healthier with our Citrus Glazed Salmon with Pecan-Citrus Rice dish. Many people know that fatty fish like salmon and mackerel are rich in nutrients. However, most aren’t aware that they’re also good for people with high cholesterol levels. That’s because the pink salmon fish is a great source of omega-3 fatty acids which are excellent for the heart. In particular, the salmon’s omega-3 fatty acids can help boost good cholesterol and help lower the risks of getting a stroke.
Its choice of ingredients isn’t just healthy either, they’re used to complement the dish and boost its overall flavor. Paired with soft, delectable brown rice, this scrumptious seafood dish makes for a filling and nutritious meal. Aside from salmon, this recipe also uses orange and grapefruit juices for its glaze, which are also good for lowering cholesterol levels. It’s also worth mentioning that this salmon is cooked through broiling and not frying. Research shows that out of the two, broiling is the healthier method of cooking seafood like salmon.
Recipe for Inspiration: Citrus Glazed Salmon with Pecan-Citrus Rice
Barley-Herb Casserole

Next on this list of low cholesterol recipes is our Barley-Herb Casserole recipe. Casserole dishes are popular comfort food to many, and it’s no wonder why. Casseroles usually make for a hearty and filling dish. And served warm, they’re the kind of effortlessly-delicious meals that are perfect for family dinners. This casserole recipe uses healthy whole grains like barley. Similar to oats, barley helps lessen the risk of heart diseases, as well as stroke.
Asides from barley, this dish also has legumes like chickpeas which can lessen the bad cholesterol in the body. It also has vegetables like squash, tomatoes, onions, as well as parsley and rosemary. And true to being a casserole dish, it’s an easy one-pot meal that’s good for 4 people.
Recipe for Inspiration: Barley-Herb Casserole
Oatmeal With Fresh Blueberries

Who says Starbucks can’t make healthy food? Our Copycat Starbucks Oatmeal With Fresh Blueberries recipe is definitely healthier and tastier since it’s homemade. But not only that: it uses oatmeal, blueberries, and orange zest which are both foods that lessen the amount of bad cholesterol in the body. This delicious breakfast meal is perfect for mornings when you need an extra boost of energy to get through the day.
Whipping up a bowl of healthy oatmeal is also quick and easy. Just cook your oatmeal the usual way, then add some honey, cinnamon, fresh blueberries, grated orange zest, and almond milk. In just 10 minutes, you have a lovely breakfast meal that’s delectable as well as a low cholesterol recipe.
Recipe for Inspiration: Copycat Starbucks Oatmeal With Fresh Blueberries
Chocolate Orange Fondue

It may not seem obvious, but both cocoa and dark chocolate can actually lower the bad cholesterol levels in your body. And not only that, eating dark chocolate can also decrease blood pressure and even increase the amount of good cholesterol in the body. Usually, chocolate desserts become unhealthy when they’re mixed with loads of sugar, which can also be bad for your heart.
Fortunately, we don’t use sugar in this Chocolate Orange Fondue recipe. This delicious fondue uses ingredients that can both lower bad cholesterol and increase good cholesterol! It has melted dark chocolate, as well as freshly squeezed orange juice, orange zest, and orange liqueur. So if you thought that you’d say goodbye to your days of eating sweet, gooey chocolate desserts, then you’re in luck. With our recipe, you can still enjoy the sweet stuff without worry or guilt! Usually, the healthy kind of chocolate contains at least 75% cocoa content. Thankfully, this recipe requires the same amount for it to have the best result. So rest assured that you’ll be having a healthy treat despite it tasting sweet and chocolatey.
Recipe for Inspiration: Chocolate Orange Fondue
Armenian Stuffed Eggplant (Imam Bayildi)

And last but not least is our Armenian Stuffed Eggplant (Imam Bayildi) recipe. Like carrots, eggplants are pectin-rich vegetables that contain soluble fiber. When eaten, this type of fiber helps lower cholesterol levels by up to 10% by stopping the liver from producing it naturally. Asides from this, eggplants also have many other health benefits. They’re rich in vitamins and minerals, can help with digestion, and helps boost heart health.
This stuffed eggplant recipe is not only healthy, it’s savory and flavorful as well. Free from any meat ingredients, its stuffing is loaded with onions, tomatoes, parsley, and spices like cinnamon, red chili flakes, as well as fresh parsley. You’ll really get a glimpse of the wonders of Mediterranean cuisine with this eggplant dish.
Recipe for Inspiration: Armenian Stuffed Eggplant
Lentil and Chestnut Soup

Looking for more healthy, low cholesterol soup? Then look no more! This comforting dish is not only low in cholesterol, it’s also protein-rich as well.
Lentil, one of the main ingredients featured in this recipe, is also a well-known member of the legume family. As previously mentioned, legumes are good at lowering the levels of LDL or bad cholesterol in one’s body. Chestnuts, the other main ingredient, as well as other types of nuts, can do this too, making this meal perfect for when you’re on this type of diet.
Not to mention, this tasty and hearty soup is as filling and delicious as it is good for your heart’s health and body. It’s also completely easy to make too!
Recipe for Inspiration: Best Lentil and Chestnut Soup
Low-Fat Trifle

Here’s another recipe that’s not just low cholesterol. If you’re craving for some dessert, then try this low-fat trifle both diabetics and those looking after their heart health can enjoy! This fruity English treat has all you could expect from a usual trifle. Only, the ingredients are a lot more light and healthier so you can eat dessert practically guilt-free.
Aside from spongy cake, custard, and milk, the other main features of this dish include strawberries and berries. Strawberries are rich in a type of soluble fiber called pectin which can help lower the body’s cholesterol levels. Berries, too, have plant compounds that can increase levels of good cholesterol and do the opposite for bad cholesterol. Not only that, but these compounds can also prevent heart diseases from even forming in the first place thanks to their antioxidant abilities.
Recipe for Inspiration: Low-Fat Trifle
Chicken Fajitas

You can still indulge in hearty and flavorful meals like fajitas even when you’re on a low cholesterol diet! Just make sure you choose this recipe for a healthy chicken fajitas dish. Instead of the usual beef and tortillas, this dish uses chicken meat and quinoa.
While it’s true that poultry like chicken contains way less cholesterol than beef, home cooks should still be careful in which cuts they use. Some parts of chicken have more cholesterol than other areas. Generally, the breast part contains the least amount, so if you’re going to make this recipe, then make sure that the strips are from the breast part.
Recipe for Inspiration: Healthy Chicken Fajitas
High Fiber Oatmeal

Here’s another low-cholesterol oatmeal recipe you might want to try for breakfast. This high fiber meal is filled with all kinds of healthy whole grains like barley and oats which are all good for one’s heart. There’s also rye, wheat, and your choice of berries, whether it be cranberries, blueberries, or raisins. It’s very easy to whip up and is perfect if ever you’re in need of a fast but filling breakfast meal.
Recipe for Inspiration: Mill Cottage’s Ultimate High Fiber Oatmeal
Chocolate Fudge Banana Muffins

You can also have some delicious chocolatey muffins for breakfast in case you need something to-go. This recipe for banana muffins are perfect as desserts too! Also, did we mention that they’re incredibly healthy as well? You won’t need to worry about a thing when you’re munching on these choco muffin treats.
For a low cholesterol diet-friendly version, this recipe uses whole wheat flour instead of the usual all-purpose flour. And for the choco flavors, some unsweetened cocoa powder. Like dark chocolate, cocoa powder is also good for those on a low-cholesterol diet. It has zero cholesterol and contains substances called flavonoids which can help protect one from developing heart diseases. They also have antioxidants that help balance the cholesterol levels in one’s body.
Recipe for Inspiration: Chocolate Fudge Banana Muffin
Teriyaki Tofu

Another type of food that can actually help lower cholesterol is soy-based foods like tofu and soy milk. Not only that, they’re also a good source of protein aside from meat and dairy. And with this recipe in hand, you’ll get to enjoy wonderfully pressed and firm tofu marinated in delicious Japanese-inspired teriyaki sauce.
This dish is not only easy to make, but it’s also a good recipe to try in case you’re struggling to feed the kids some nutritious meals. So in case you whip up some of these scrumptious teriyaki tofu triangles for your low cholesterol diet, the whole family can join in on the healthy food experience too.
Recipe for Inspiration: Teriyaki Tofu Triangles
Sautéed Spinach and Kale

Green, leafy vegetables like spinach and kale are a healthy food source for just about anyone. However, they’re even better for those looking after their body’s cholesterol levels. Both contain vitamins called lutein as well as other carotenoids that can actually protect you from heart diseases.
And with this yummy recipe in hand, you won’t have to second-guess how to serve these leafy greens ever again. In this dish, baby spinach and kale are sauteed along with olive oil, crushed basil, and aromatic garlic for a truly inspiring dish. It’s quick to prepare and is a staple must-try in any low cholesterol diet list!
Recipe for Inspiration: Sautéed Spinach and Kale
Cod With Quinoa

Fish like cod are a good source of omega-3 fatty acids which can help lower LDL or bad cholesterol levels in one’s body. And not only are they healthy. They’re also a good alternative to the usual chicken, pork, or beef in one’s every day diet as well. This recipe also ups the ante of how you usually serve cod by covering it with an irresistible honey soy glaze. It’s then enjoyed along with healthy quinoa for a truly filling meal.
Recipe for Inspiration: Honey Soy Glazed Cod With Quinoa
Lemon Chicken
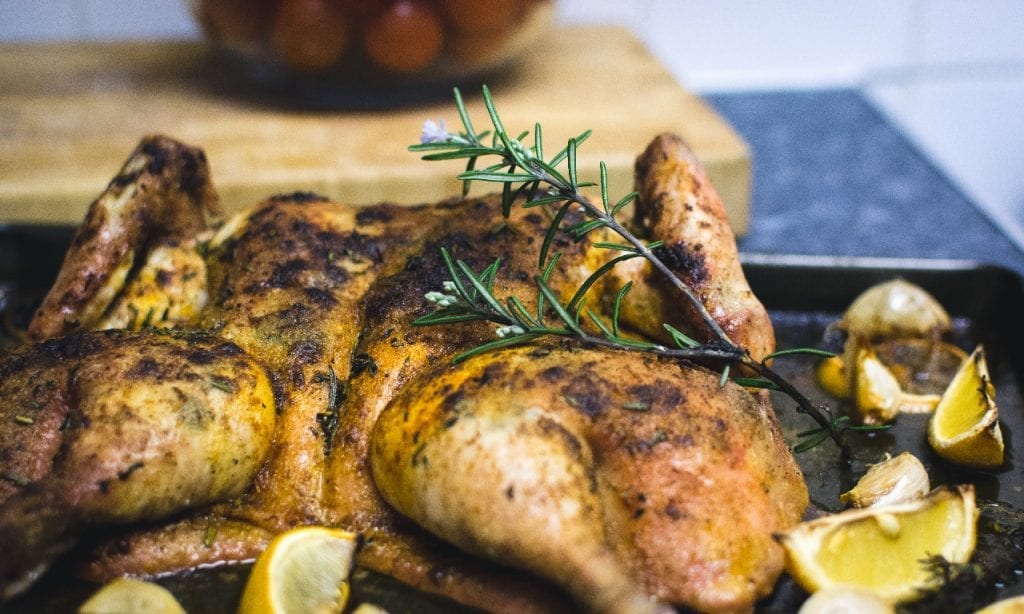
Aside from vegetables and berries, citrus fruits like lemon can also help lower the body’s cholesterol levels. And if you’re thinking of how to incorporate lemon into your meals, then look no further. This recipe for peppered lemon chicken is quick to whip up and incredibly tasty too! Not only does lemon’s citrusy flavor bring a unique punch to how you serve chicken. It also helps to tenderize the poultry, giving you truly delicate meat.
Recipe for Inspiration: Peppered Lemon Chicken
Grilled Okra

This recipe for grilled okra is simple, but it works. Like vegetables and berries, okra or ladyfingers is a low-calorie veggie that’s also a good source of soluble fiber. This soluble fiber actually helps lessen the amount of cholesterol that your body absorbs. This makes it a wonderful food to include in your low cholesterol diet.
While there are many ways to serve okra, grilling it is not only easy. It also imparts a smoky flavor that’ll make the vegetable taste even better. This is a good recipe to try in case you have cook outs with your buddies, too!
Recipe for Inspiration: Grilled Okra
Dark Chocolate Avocado Mousse

Craving for something soft and chocolatey? Enjoy a healthy version of the classic French dessert, mousse, with this recipe. It uses both heart-healthy foods, cocoa and avocado, to give you an irresistible after-meal treat.
For the cocoa, unsweetened cocoa powder and baking chocolate with 70 percent cocoa is used. These are some of the healthiest forms of chocolate you can ever eat since there’s more cocoa than milk or sugar in it.
In addition, this recipe also uses ripe avocado fruits. It’s not only good for those looking after their heart health but also adds a creamy texture to the irresistible mousse dessert.
Recipe for Inspiration: Dark Chocolate Avocado Mousse
Grilled Salmon

This seafood dish is not only heart-friendly, it’s also good for diabetics as well. Aside from cod, another kind of fish you can include in your low cholesterol diet is salmon. Salmon is a type of fatty fish that can provide numerous health benefits because of its vitamin and mineral content. Not only can it help with weight loss, but it can also help lower cholesterol levels in your body.
In this recipe, salmon fillets are brushed with a lemon-and-garlic coating, then grilled along with crunchy asparagus. It doesn’t take long to prepare, much less cook, this dish. So if you’re in a rush or lack the energy to do intense, healthy cooking, look no further than this smoky grilled salmon dish!
Recipe for Inspiration: Diabetic-Friendly Grilled Salmon
Lentil Salad

As previously stated, legumes like lentils and chickpeas can effectively reduce the bad cholesterol levels in your body. Both lentils and chickpeas are also a good source of plant-based protein. And not only are they healthy, lentils (in particular) are also incredibly easy to make! Just boil or simmer ‘em and they’re done.
But just because they’re easy to make, doesn’t mean we can’t get creative with how they’re served. This Moroccan-inspired chilled lentil salad shows you a glimpse of North African cuisine. It uses ingredients like bell peppers, lime, and cilantro to get the freshest flavors. So, if you’re looking for something nutritious yet filling for lunch, then you should definitely try this salad recipe.
Recipe for Inspiration: Moroccan Lentil Salad
Crockpot Oatmeal

flickr | monica.shaw
You’ll need your handy crockpot ready for this brilliant breakfast dish. In this recipe, heart-healthy ingredients such as steel-cut oats, apples, raisins, and walnuts are tossed into the crockpot to slow-cook overnight. What awaits you in the morning is probably the best-tasting oatmeal breakfast you’ll ever taste!
If you wish, you can replace the steel-cut oats with old-fashioned rolled ones. However, the steel-cut oats have the best texture and flavor that goes with this creamy and healthy dish! So start your day right with this crockpot oatmeal recipe.
Recipe for Inspiration: Deluxe Crockpot Oatmeal
Vinegar-Marinated Green Beans

Want something light for lunch? How about a heart-healthy appetizer for dinner parties? Then look no further! These vinegar-marinated green beans fit the bill perfectly. The green beans are first boiled until completely tender. Then they’re marinated in white and balsamic vinegar to complement the crunchy texture of the green veggies. The vinegar is able to bring acidic yet exciting flavors that’s sure to keep you wanting more.
Recipe for Inspiration: Vinegar-Marinated Green Beans
Chickpea Burger

Craving for a scrumptious burger, but don’t want the extra cholesterol that comes with it? Then try incorporating chickpea into your meals for a low cholesterol diet. Don’t worry, these legumes are great for burgers too!
This recipe needs two cups of chickpea that are mashed together to form a burger patty. Just cook it as you would ground beef and you’ll have a healthy alternative for the notorious fast-food staples that you love as a snack or as a complete meal.
Recipe for Inspiration: Chickpea Burger
Spaghetti with Mackerel and Nuts

Here’s a healthy twist to one of your favorite spaghetti recipes. This dish substitutes meat with mackerel, pine nuts, and golden raisins. These nutritious additions help lower bad cholesterol levels in your body, while providing you with healthy cholesterol too!
To make this recipe, you have to pan-fry the mackerel, incorporate water into the raisins and stir them in with the rest of the ingredients. And the best part about this recipe is that it whips up in a snap too!
Recipe for Inspiration: Spaghetti with Mackerel and Pine Nuts
Barley and Oat Pancakes

While some of the recipes above help curb your hunger and savory cravings, this one is a filling and healthy breakfast! Instead of the usual flour, you’ll substitute it with barley flour that’s definitely a healthier option. Not only does this pancake make a filling breakfast but it is also low in cholesterol. In our opinion, barley flour is a good addition to have in your pantry.
Barley contains fiber that’s found in fruits, vegetables, and oats. And as it turns out, this recipe contains oats too. Hand in hand, they’ll help lower your cholesterol.
Recipe for Inspiration: Barley Oat Pancakes
Roasted Vegetables
Vegetables like zucchini and eggplant are rich in carotenoids that help avoid heart diseases. Besides carotenoids, these vegetables are also rich in fiber and potassium that help lower blood pressure and cholesterol. Moreover, nothing says healthy as well as this recipe that contains eggplant and zucchini!
And to top it all off, this one is roasted! Make it a tad bit healthier by replacing salad dressing mix with your homemade salad dressing!
Recipe for Inspiration: Simple Roasted Vegetables
Strawberry and Broccoli Smoothie

Another addition to your low cholesterol diet is this strawberry and broccoli combo. But unlike other recipes from this list, this one is sweet despite being healthy! Most of all, it’s refreshing and so easy to make. Making it a good recipe for those always on the go!
In addition to having properties for lowering your cholesterol, this also provides you with a healthy dose of vitamin C. And so although this one comes in a sweet yet refreshing drink, it’s packed with healthy nutrients that give one a balanced diet.
Recipe for Inspiration: Healthy Strawberry and Broccoli Smoothie
Carrot Oat Cookies

On the lookout for more healthy desserts, you can add to your low cholesterol diet? We found two perfect ingredients for dessert that don’t compensate taste: carrots and oats. And they complement each other too and are used together in several dessert recipes. But not only do they help you with LDL cholesterol levels, but oatmeal cookies are also low-calorie! Hit two heads with one stone with this healthy dessert alternative.
Recipe for Inspiration: Carrot Oat Cookies
Granola

A low cholesterol diet does not equate to having a dull and boring breakfast. Aside from pancakes, you can also add granola to your low cholesterol food list. Granola mixed with some fruits like oranges, cranberries, and nuts packs a lot of nutrients such as iron, zinc, and magnesium.
However, many granola brands in the market do not contain enough oats. Make it a habit to check the ingredients list first when looking for a new brand. Or better yet, make your own granola using our recipe. They’re healthier too compared to store-bought granolas.
Recipe for Inspiration: Cranberry Orange Granola
Orange Sorbet Smoothie

Just because you’re planning to be healthy doesn’t mean you can’t enjoy a good and refreshing glass of this orange smoothie! After all, there are fruits you can use that can help you fight high levels of LDL or bad cholesterol.
One of the fruits we find that is low in cholesterol is orange. In this recipe, orange-flavored sorbet is combined with other fruits such as grapefruit, strawberry, and pineapple to make a refreshingly icy smoothie. And the best thing is that sorbet is actually a healthy alternative to ice cream!
Recipe for Inspiration: Orange Sorbet Smoothie
Watermelon Sorbet

Not only is sorbet a healthy alternative for ice cream, but it also helps in lowering your fat and caloric intake since it doesn’t have dairy in it. Meaning, it is completely ice-based. Since there’s no dairy, sorbet also makes a safe addition to your low cholesterol diet.
Sorbet comes in an assortment of fruity flavors so it is really up to you what flavor or fruit juice you wish to try. To start, you can try our watermelon sorbet recipe for a perfect summer treat!
Recipe for Inspiration: Watermelon Sorbet
Grilled Tuna

Flickr | Jari Kurittu
If you’re into losing weight, you probably already know tuna is healthy, and it’s incredibly high in protein despite being low in calories. Additionally, though, tuna is also a good source of omega-3 fatty acids that helps you manage your cholesterol levels.
Tuna is astonishingly versatile too, so you’ll have no problem incorporating this into your diet right away. But many who watch their weight opt for grilled recipes like our grilled tuna with fresh tomato salsa.
Recipe for Inspiration: Grilled Tuna with Fresh Tomato Salsa
Conclusion
You won’t have to worry about your cholesterol levels ever again with our low cholesterol diet recipes. With healthy ingredients that lower cholesterol and protect your heart from diseases, our recipes have proven that you can enjoy your meals and take care of your health all at the same time.
Was this page helpful?
Read Next: 9 Herbal Tea Benefits and Best Types of Herbal Tea to Drink
Naomi Blue
Naomi is a writer, editor, and manga enthusiast. She has written for various websites, events, and ad commercials. She is also an avid fan of street food and food history. She’s currently in her Japanese and Indonesian food phase and is interested in exploring Vietnamese cuisine next.













