
1 hr
1
2
3
4
5
5
from
1
vote
Eating healthy has never been more delightful with these low cholesterol recipes! These are dishes with less fat, but has yet to sacrifice mouthwatering flavors. We have it all from delectable sweet and savory like sugar-free pies and hearty casseroles. There is never a shortage of these healthy but truly appetizing low cholesterol recipes.
Read More

1 hr 15 mins
1
2
3
4
5
5
from
1
vote
This Hainan-style steamed ginger chicken makes super tender and flavorful steamed chicken with ginger soy dipping sauce. It's an easy to make dinner for the family.

1 hr 30 mins
1
2
3
4
5
5
from
2
votes
Enjoy an elegant plate of savory glazed salmon over citrusy sweet pecan rice. Try making it and serve a delicious seafood meal for lunch or dinner in less than 2 hours.
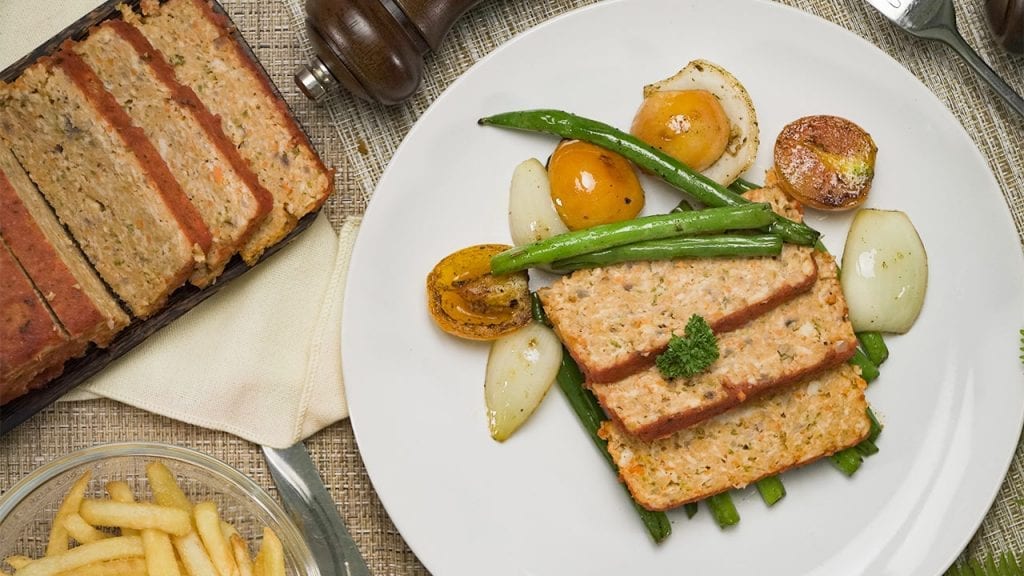
1 hr 35 mins
1
2
3
4
5
5
from
3
votes
Eat healthy with our tender and savory low cholesterol chicken meatloaf. Mixed with veggies and marinara sauce, this meatloaf is moist and delicious!
Read More

2 hrs
1
2
3
4
5
5
from
2
votes
A satisfyingly healthy and tasty stuffed eggplant casserole with flavorful tomato sauce, oil and spices, baked to perfection.


1 hr 30 mins
1
2
3
4
5
5
from
1
vote
Using just five ingredients, you can create this stunning and simple autumn dessert that's flavorful even without the added sugar.

1 hr 40 mins
1
2
3
4
5
5
from
3
votes
An amazing one-pot meal loaded with nutrients, comforting barley, and lots of other vegetables and spices.

10 mins
1
2
3
4
5
5
from
2
votes
Chill out with this chilled avocado soup recipe. Creamy avocado blended with fresh cucumber and bright lime juice for a dish that will help you stay cool.
Read More

15 mins
1
2
3
4
5
5
from
3
votes
This tasty veggie dish will make you love taste of broccoli. All you need to do is add some almonds and you're good to munch it all up.
Read More










